Note
Click here to download the full example code
Stationnary vortex¶
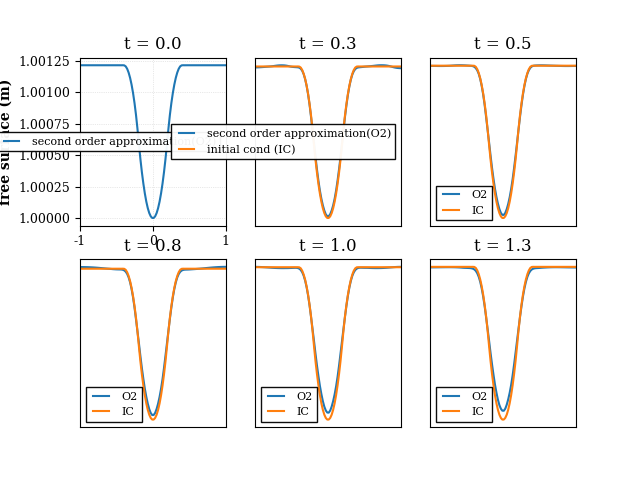
In this example, we test the conservation of the geostrophic equilibrium by conserving a stationnary vortex. The test case is already discribed in [10] and [11] (see References).
import os, sys
from os import listdir
import argparse
import matplotlib.pylab as plt
import freshkiss3d as fk
import freshkiss3d.extra.plots as fk_plt
import numpy as np
import matplotlib.tri as mtri
from scipy.interpolate import griddata
from matplotlib import colors
import matplotlib.ticker as mtick
import h5py
import math
#sphinx_gallery_thumbnail_number = 2
parser = argparse.ArgumentParser()
parser.add_argument('--nographics', action='store_true')
args = parser.parse_args()
fk_plt.set_rcParams()
def plot_free_surface_slice(triangular_mesh, H, topography, fig,
nb_l, nb_c, plt_num,
time, Eta0_slice=None, label=True):
# Plt options:
n = 100
TG = triangular_mesh.triangulation
x_slice = np.linspace(min(TG.x), max(TG.x), n)
ym_slice = np.full(n, (max(TG.y) + min(TG.y)) / 2.0)
NC = triangular_mesh.NV
Eta = np.empty(NC, dtype='d')
for C in range(NC):
Eta[C] = H[C] + topography[C]
Eta_slice = griddata((TG.x, TG.y), Eta, (x_slice, ym_slice), method = 'cubic')
ax = fig.add_subplot(nb_l, nb_c, plt_num)
ax.xaxis.set_major_formatter(mtick.FormatStrFormatter('%d'))
if label:
ax.plot(x_slice, Eta_slice, label='second order approximation(O2)')
else:
ax.plot(x_slice, Eta_slice, label='O2')
if Eta0_slice is not None:
if label:
ax.plot(x_slice, Eta0_slice, label='initial cond (IC)')
else:
ax.plot(x_slice, Eta0_slice, label='IC')
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax.set_xlim([min(x_slice), max(x_slice)])
ax.set_ylabel("free surface (m)")
ax.set_title("t = {:.1f}".format(time))
ax.legend(loc='best')
return Eta_slice
dir_path = os.path.abspath(os.path.dirname(sys.argv[0]))
Analytic solution:¶
The hydrostatic Euler with Coriolis and constant density is given by
\[\begin{split}\begin{cases}
\nabla\cdot {\bf U} = 0, \\
\rho_0\left(\frac{\partial {\bf u}}{ \partial t} + \nabla_{x,y}\cdot ( {\bf u}\otimes {\bf u}) +
\frac{\partial ({\bf u}w)}{\partial z}\right) + \nabla_{x,y} p = -\rho_0\Omega {\bf u}^\perp, \\
\frac{\partial p}{\partial z} = -\rho_0 g.
\end{cases}\end{split}\]
First, we consider the reference case given in polar coordinates. In this case, the problem is initialized with the velocity \({\bf{u}}^0\) and the water height \(h^0\),
\[\begin{split}\begin{cases}
{\bf{u}}^0(r,\theta) = {\bf{\nu}}(r) \bf{e_\theta},\\
\partial_r h^0(r) = \frac{\nu(r)}{g} \left(\Omega + \frac{\nu(r)}{r} \right),
\end{cases}\end{split}\]
with:
\[{\bf{\nu}} (r) = (\alpha r \mathbb{1}_{r<R} \ + \ \alpha(2R - r)\mathbb{1}_{R\leq r < 2R}).\]
In cartesian coordinates, this gives :
\[\begin{split}\begin{cases}
u^0(x,y,z,t) = - \frac{y}{\sqrt{x^2 + y^2}} \nu \left(\sqrt{x^2 + y^2}\right), \\
v^0(x,y,z,t) = \frac{x}{\sqrt{x^2 + y^2}} \nu \left(\sqrt{x^2 + y^2}\right), \\
h^0(x,y,z,t) = h^0(\sqrt{x^2 + y^2}).
\end{cases}\end{split}\]
with:
\[h^0(r) = \left(\frac{5 \varepsilon \Omega}{g} + \frac{25 \varepsilon^2}{g} ln(r)\right) \mathbb{1}_{r<1/5}\]
\[+ \left(\frac{\varepsilon}{g} (2r - \frac{5}{2}r^2) \Omega + \frac{\varepsilon^2}{g}(4ln(r) - 20r + 12.5 r^2) \right) \mathbb{1}_{1/5\leq r < 2/5}.\]
def hVortex(r, h0):
if 0. <= r and r <= 0.2:
return h0 + (omega + 5 * eps) * (r ** 2) * 2.5 * eps / g
elif 0.2 < r and r <= 0.4:
return hVortex(0.2, h0) + eps * \
omega / g * (2 * r - 2.5 * (r ** 2) - 0.3) \
+ (eps ** 2) / g * (4 * np.log(5 * r) - 20 * r + 12.5 * r ** 2 + 3.5)
elif 0.4 < r:
return hVortex(0.4, h0)
def uVortex(r): # u_theta
return eps * (5 * r * (r <= 0.2) + (2 - 5 * r) * (0.2 < r and r <= 0.4))
Parameters:¶
We assume that \(\rho = \rho_0 = 1\). In the [11], authors of choose \(\alpha = 5 \varepsilon\), where \(\varepsilon\) controls the depth of the vortex, and \(R = \frac{1}{5}\).
\[\begin{split}\begin{cases}
\Omega = 1, \\
g = 9.81, \\
h^0 = 1, \\
z_b^0 = 0, \\
\varepsilon = 0.05.
\end{cases}\end{split}\]
# Non-linear vortex:
omega = 1. # angular velocity
#Let us consider two cases:
#
# * In the first case we use a semi-implicite in time method
# * In the second case we use the apparent topography method, the method is only implemented for the order 1.
#
case = 1
if case == 1:
NUM_PARAMS={'space_second_order':True}
PHY_PARAMS={'coriolis_effect':True, 'apparent_topo':False}
if case == 2:
NUM_PARAMS={'space_second_order':False}
PHY_PARAMS={'coriolis_effect':True, 'apparent_topo':True}
g = 9.81
h0 = 1. # initial water height
eps = 0.05 # controls the depth of the vortex
# the smaller it is, the closer you are to the linear
Time loop:¶
FINAL_TIME = 1.5
simutime = fk.SimuTime(final_time=FINAL_TIME, time_iteration_max=1000000,
second_order=True)
restart_times = [0., 0.25, 0.5, 0.75, 1., 1.25]
restart_scheduler = fk.schedules(times=restart_times)
Mesh:¶
Also we consider a square domain \([-1, 1] \times [-1, 1]\), the average edge length of the mesh equals to 0.04.
os.system('gmsh -2 -format msh2 inputs/tiny_square.geo -o inputs/tiny_square.msh')
triangular_mesh = \
fk.TriangularMesh.from_msh_file(
dir_path + '/inputs/tiny_square.msh')
hm = 0.04
Layers:¶
NL = 1
layer = fk.Layer(NL, triangular_mesh, topography=0.)
LAYER_IDX = int(NL/2)
Primitives:¶
NC = triangular_mesh.NV
x = triangular_mesh.vertices.x
y = triangular_mesh.vertices.y
h_init = np.empty(NC, dtype='d')
hu_init = np.empty((NC, NL), dtype='d')
hv_init = np.empty((NC, NL), dtype='d')
for C in range(NC):
rt = np.sqrt(x[C] ** 2 + y[C] ** 2)
al = np.arctan2(y[C], x[C])
h_init[C] = hVortex(rt, h0)
for L in range(NL): # Correct for only one layer
hu_init[C,L] = h_init[C] * (-np.sin(al) * uVortex(rt))
hv_init[C,L] = h_init[C] * (np.cos(al) * uVortex(rt))
primitives = fk.Primitive(triangular_mesh, layer,
height=h_init,
QXinit=hu_init,
QYinit=hv_init,
Coriolis_coeff=omega)
Boundary conditions:¶
slides = [fk.Slide(ref=r) for r in [1, 2, 3, 4]]
Writter:¶
vtk_writer = fk.VTKWriter(triangular_mesh,
scheduler=fk.schedules(count=10), scale_h=10.)
h5_writer = fk.H5Writer(scheduler=restart_scheduler, \
output_dir='outputs/hydrodynamic_h5_vortex')
Problem definition:¶
problem = fk.Problem(simutime, triangular_mesh,
layer, primitives,
slides=slides,
numerical_parameters=NUM_PARAMS,
physical_parameters=PHY_PARAMS,
vtk_writer=vtk_writer,
h5_writer=h5_writer,
)
===================================================================
| INITIALIZATION |
===================================================================
Problem size: Nodes=3014, Layers=1, Triangles=5826,
Iter = 0 ; Dt = 0.0000s ; Time = 0.00s ; ETA = 0.00s
Problem solving:¶
problem.solve()
===================================================================
| TIME LOOP |
===================================================================
Iter = 26 ; Dt = 0.0012s ; Time = 0.03s ; ETA = 12.92s
Iter = 51 ; Dt = 0.0012s ; Time = 0.06s ; ETA = 12.46s
Iter = 76 ; Dt = 0.0012s ; Time = 0.09s ; ETA = 12.30s
Iter = 101 ; Dt = 0.0012s ; Time = 0.12s ; ETA = 11.90s
Iter = 126 ; Dt = 0.0012s ; Time = 0.15s ; ETA = 11.33s
Iter = 151 ; Dt = 0.0012s ; Time = 0.18s ; ETA = 10.75s
Iter = 176 ; Dt = 0.0012s ; Time = 0.22s ; ETA = 10.64s
Iter = 201 ; Dt = 0.0012s ; Time = 0.25s ; ETA = 10.42s
Iter = 226 ; Dt = 0.0012s ; Time = 0.28s ; ETA = 10.09s
Iter = 251 ; Dt = 0.0012s ; Time = 0.31s ; ETA = 9.86s
Iter = 276 ; Dt = 0.0012s ; Time = 0.34s ; ETA = 9.43s
Iter = 301 ; Dt = 0.0012s ; Time = 0.37s ; ETA = 9.33s
Iter = 326 ; Dt = 0.0012s ; Time = 0.40s ; ETA = 9.09s
Iter = 351 ; Dt = 0.0012s ; Time = 0.43s ; ETA = 8.75s
Iter = 376 ; Dt = 0.0012s ; Time = 0.46s ; ETA = 8.45s
Iter = 401 ; Dt = 0.0012s ; Time = 0.49s ; ETA = 8.22s
Iter = 426 ; Dt = 0.0012s ; Time = 0.52s ; ETA = 7.98s
Iter = 451 ; Dt = 0.0012s ; Time = 0.55s ; ETA = 7.96s
Iter = 476 ; Dt = 0.0012s ; Time = 0.58s ; ETA = 7.66s
Iter = 501 ; Dt = 0.0012s ; Time = 0.61s ; ETA = 7.45s
Iter = 526 ; Dt = 0.0012s ; Time = 0.64s ; ETA = 7.18s
Iter = 551 ; Dt = 0.0012s ; Time = 0.67s ; ETA = 6.85s
Iter = 576 ; Dt = 0.0012s ; Time = 0.71s ; ETA = 6.60s
Iter = 601 ; Dt = 0.0012s ; Time = 0.74s ; ETA = 6.32s
Iter = 626 ; Dt = 0.0012s ; Time = 0.77s ; ETA = 6.13s
Iter = 651 ; Dt = 0.0012s ; Time = 0.80s ; ETA = 5.87s
Iter = 676 ; Dt = 0.0012s ; Time = 0.83s ; ETA = 5.56s
Iter = 701 ; Dt = 0.0012s ; Time = 0.86s ; ETA = 5.36s
Iter = 726 ; Dt = 0.0012s ; Time = 0.89s ; ETA = 5.13s
Iter = 751 ; Dt = 0.0012s ; Time = 0.92s ; ETA = 4.77s
Iter = 776 ; Dt = 0.0012s ; Time = 0.95s ; ETA = 4.51s
Iter = 801 ; Dt = 0.0012s ; Time = 0.98s ; ETA = 4.32s
Iter = 826 ; Dt = 0.0012s ; Time = 1.01s ; ETA = 3.95s
Iter = 851 ; Dt = 0.0012s ; Time = 1.04s ; ETA = 3.79s
Iter = 876 ; Dt = 0.0012s ; Time = 1.07s ; ETA = 3.50s
Iter = 901 ; Dt = 0.0012s ; Time = 1.10s ; ETA = 3.26s
Iter = 926 ; Dt = 0.0012s ; Time = 1.13s ; ETA = 3.04s
Iter = 951 ; Dt = 0.0012s ; Time = 1.16s ; ETA = 2.78s
Iter = 976 ; Dt = 0.0012s ; Time = 1.19s ; ETA = 2.50s
Iter = 1001 ; Dt = 0.0012s ; Time = 1.23s ; ETA = 2.27s
Iter = 1026 ; Dt = 0.0012s ; Time = 1.26s ; ETA = 2.03s
Iter = 1051 ; Dt = 0.0012s ; Time = 1.29s ; ETA = 1.76s
Iter = 1076 ; Dt = 0.0012s ; Time = 1.32s ; ETA = 1.51s
Iter = 1101 ; Dt = 0.0012s ; Time = 1.35s ; ETA = 1.26s
Iter = 1126 ; Dt = 0.0012s ; Time = 1.38s ; ETA = 0.99s
Iter = 1151 ; Dt = 0.0012s ; Time = 1.41s ; ETA = 0.75s
Iter = 1176 ; Dt = 0.0012s ; Time = 1.44s ; ETA = 0.51s
Iter = 1201 ; Dt = 0.0012s ; Time = 1.47s ; ETA = 0.25s
Iter = 1226 ; Dt = 0.0002s ; Time = 1.50s ; ETA = 0.00s
===================================================================
| END |
===================================================================
Problem.solve() completed in 14.015119075775146s (wall time)
Plot the data saved¶
TIMES = []
H_t = []
filenames = [f for f in listdir('./outputs/hydrodynamic_h5_vortex')]
filenames = ['./outputs/hydrodynamic_h5_vortex/' + f for f in filenames]
order = [int(f[-4]) for f in filenames]
filenames = [f for _,f in sorted(zip(order, filenames))]
for filename in filenames:
h5_reader = fk.H5Reader(filename = filename)
x,_y, time, time_it_, H, U, V, W, HL, QX, QY, Rho, \
topography , Hn, Un, Vn, \
HLn, QXn, QYn, T, HT, Tn, HTn, positions, velocities = \
h5_reader.read_solution()
TIMES.append(time)
H_t.append(H)
if not args.nographics:
nb_l = 2
nb_c = 3
pos = 1
fig = plt.figure(1)
Eta0_slice = plot_free_surface_slice(\
triangular_mesh, H_t[0], topography, fig,
nb_l, nb_c, pos, TIMES[0])
N_TIMES = len(TIMES)
for i in range(1, N_TIMES):
pos += 1
label = True
if i != 1:
label = False
plot_free_surface_slice(\
triangular_mesh, H_t[i], topography, fig,
nb_l, nb_c, pos, TIMES[i], Eta0_slice=Eta0_slice, label=label
)
plt.show()
os.system('rm inputs/tiny_square.msh')
0
Total running time of the script: ( 0 minutes 15.232 seconds)